Geisha

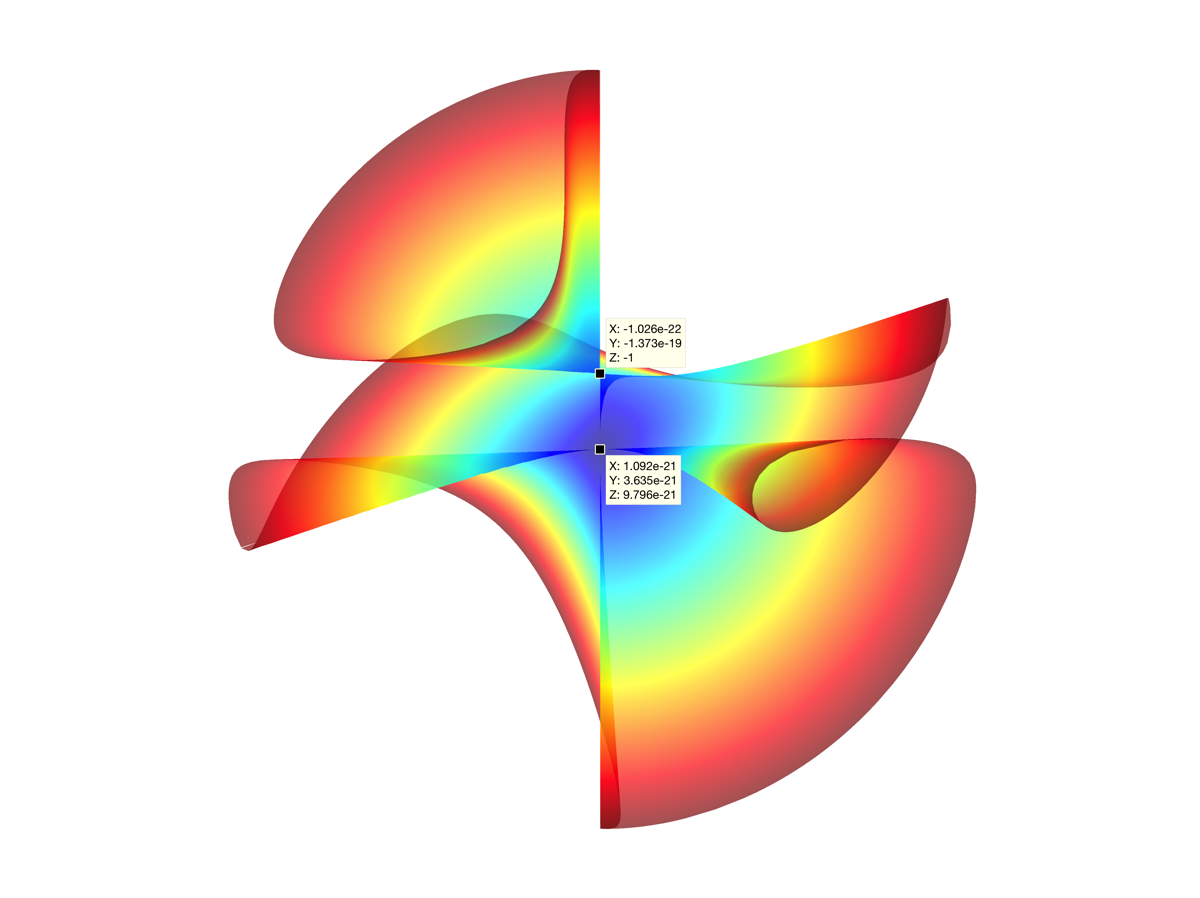
Equation
\[ x^2yz+x^2z^2 = y^3z+y^3 \]
Properties:
- degree 4
- two singular curves, both lines. one is a cusp, the other is a self-crossing. at least in terms of the real part...
- two singular points, one at the intersection of the two singular lines -- at the origin. the other is at \( (0,0,-1) \), and is a cusp singularity, lying only on the singular \(z\)-axis


Some story
The support came off quite nicely, except where the two separate bodies join, at \( (0,0,-1) \), where the printed surface broke. Not surprising. PLA is a brittle plastic, so even a little extra force while removing support is likely to break these point singularities. So I hot-glued it back together.
Sphere of radius 5, random projection.

input